Unstable-Homotopy-Forum-2025
View the Project on GitHub hrzsea/Unstable-Homotopy-Forum-2025
Unstable Homotopy Forum at AMSS
Aug. 12-16, 2025
The forum is dedicated to sharing recent advances and key techniques, fostering collaboration, formulating new problems, and inspiring interdisciplinary research in related areas such as manifolds, geometry, and algebra.
The event will take the form of a workshop-style forum, featuring 10 invited speakers, each delivering a series of two one-hour talks. This format is designed to promote deep academic communications, encourage mutual learning, and allow ample time for meaningful discussions.
(Please note this forum is paperless)
Organizers:
Ruizhi Huang, Jianzhong Pan, Zhengyi Zhou
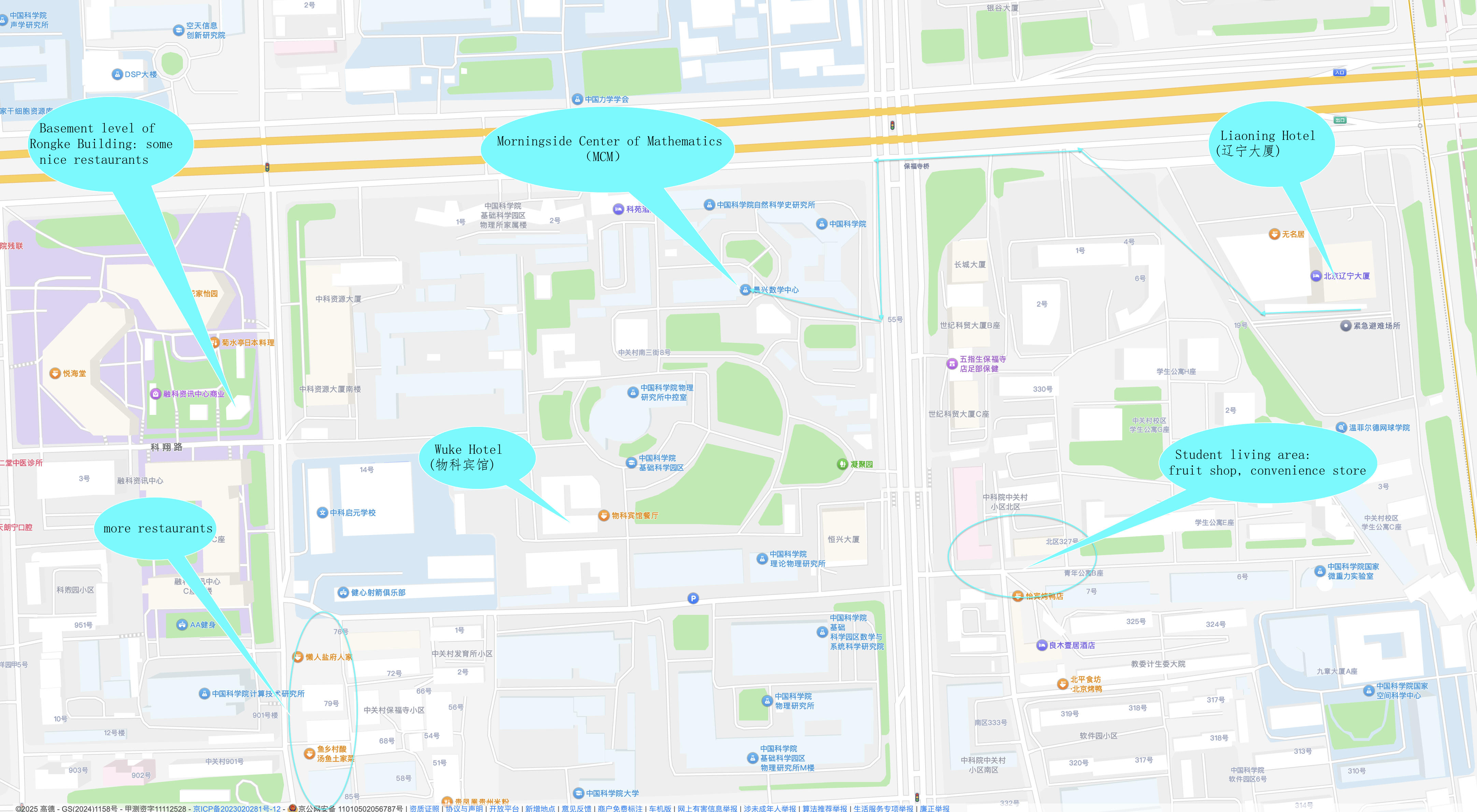
Place: MCM 110
Speakers:
Samik Basu (Indian Statistical Institute),
Guy Boyde (Utrecht University),
Xin Fu (Shanghai Institute for Mathematics and Interdisciplinary Sciences)),
Pengcheng Li (Great Bay University),
Daisuke Kishimoto (Kyushu University),
Stephen Theriault (University of Southampton),
Jiawei Zhou (Nanchang University)
Program
(Unstable Homotopy Forum)
| Aug. 12, Tue | Aug. 13, Wed | Aug. 14, Thu | Aug. 15, Fri | Aug. 16, Sat | |
|---|---|---|---|---|---|
| 9:30 - 10:30 | Haibao Duan | Jie Wu | Samik Basu | Stephen Theriault | Daisuke Kishimoto (online) |
| 10:30 - 11:00 | Tea Break | ||||
| 11:00 - 12:00 | Haibao Duan | Jie Wu | Samik Basu | Stephen Theriault | Daisuke Kishimoto (online) |
| 12:00-14:30 | Lunch Time | ||||
| 14:30 - 15:30 | Xin Fu | Guy Boyde | Sergei Ivanov | Pengcheng Li | Jiawei Zhou |
| 15:30 - 16:00 | Tea Break | ||||
| 16:00 - 17:00 | Xin Fu | Guy Boyde | Sergei Ivanov | Pengcheng Li | Jiawei Zhou |
Title and Abstract
- Samik Basu
Title: Spherical fibrations over highly connected manifolds
Abstract: A simply connected 4-manifold supports a circle bundle whose total space is a connected sum of copies of S^2 \times S^3. The proof of this relies on Smale’s classification of spin 5-manifolds. We investigate the story from a homotopy theoretic point of view, which leads to generalizations to the case of (n-1)-connected 2n-dimensional Poincare duality complexes. This is joint work with Aloke Kr. Ghosh, and also partly with Subhankar Sau.
- Guy Boyde
Title: Diagram algebras from a homological point of view
Abstract: Diagram algebras are a class of associative algebras that show up in many different areas. They solve counting problems in statistical physics, let us build knot invariants, and encode the representation theory of certain groups. Rachael Boyd and Richard Hepworth showed that families of diagram algebras often exhibit homological stability (suitably interpreted)
In these talks, I’ll aim to give a friendly introduction to some of the main families of diagram algebras (especially the Temperley–Lieb, Brauer, and partition algebras) and give a simple toolkit that allows one to establish basic stability results and compute some homology.
- Haibao Duan
Title: Integral Weyl invariants of Lie groups
Abstract: Let G be a compact connected Lie group with a maximal torus T, and let Inv(G)⊂H^{∗}(B_{T}) denote the ring of integral Weyl invariants of G, where B_{T} denotes the classifying space of T. This paper develops two complementary approaches to the structure of the ring Inv(G).
The first is an algebraic approach based on a classification of so called “integral domains with multiplicative content”, which yields an explicit description of Inv(G) in terms of a minimal set of generators and relations. The second is a geometric approach, grounded in an integral refinement of the classical divided difference operators from Schubert calculus and a classification of the parabolic subgroups of G. This method is particularly suited for reducing the computation of the ring Inv(G) to the Cartan matrix of G. As applications, we address three fundamental problems concerning the ring Inv(G) posed by Borel in 1955.
- Xin Fu
Title: Rigidity in toric topology
Abstract: Rigidity phenomena in geometry and topology concern when a weaker equivalence between two spaces implies a stronger one. A long-standing problem in toric topology asks whether quasitoric manifolds can be classified up to homeomorphism or diffeomorphism by their integral cohomology rings.
In the first half of this talk, I will survey several notions of rigidity that arise in the study of manifolds with torus actions within toric topology. In the second half, I will discuss toric spaces that exhibit a homotopical form of rigidity, based on joint work with Tseleung So, Jongbaek Song, and Stephen Theriault.
- Sergei Ivanov
Title: Bousfield-Kan completion as a codensity ∞-monad
Abstract: In this two-part talk series, we will recall the notion of the codensity monad, provide some examples, and extend the theory to the setting of ∞-categories. We will then discuss the notion of Bousfield-Kan completion and its generalizations, and show that these constructions are codensity ∞-monads of certain full ∞-subcategories within the ∞-category of spaces.
- Pengcheng Li
Title: Cohomotopy sets of manifolds
Abstract: Given a based CW complex $X$, the $n$-th cohomotopy set $\pi^n(X)$ is the set of homotopy classes of based maps from $X$ into the $n$-sphere. When $\dim(X)\leq 2n-2$, $\pi^n(X)$ has a natural abelian group structure by the Freuthendal suspension theorem. Cohomotopy sets of manifolds are of particular interest due to their connection with framed cobordism via the Pontryagin-Thom construction.
In the first part of the 2-hour-talk, we characterize cohomotopy groups of codimension $\leq 2$ for general (Poincare duality) complexes from the two aspects of homotopy theory and cobordism theory. In the second part, we present some explicit results on unstable cohomotopy sets for certain spaces, such as (1) the second cohomotopy set of simply-connected $6$-manifolds, (2) the $p$-local fourth cohomotopy sets of CW-complexes of dimension $\leq 10$, where $p\geq 5$ is a prime.
- Daisuke Kishimoto
Title: Morse inequalities for noncompact manifolds
Abstract: I will talk about joint work with Tsuyoshi Kato and Mitsunobu Tsutaya, in which we establish Morse inequalities for an infinite Galois covering over a closed manifold. Inequalities are given for a rough configuration of critical points and L^2-Betti numbers. As a corollary, we get the mean value version of Morse inequalities.
- Stephen Theriault
TitleI: Loop space decompositions for a family of Poincare Duality complexes
AbstractI: Under certain hypotheses, we prove a loop space decomposition for simply-connected Poincare Duality complexes of dimension n whose (n − 1)-skeleton is a co-H-space. This unifies many known decompositions obtained in different contexts and establishes many new families of examples. Some consequences will be discussed. This is joint work with Lewis Stanton.
TitleII: Directions in unstable homotopy theory
AbstractII: This talk will outline some possible future directions in unstable homotopy theory. This will include new perspectives on the geometry and topology of manifolds, integral approaches to aspects of rational homotopy theory, and approaches to major open problems where recent progress has been made and more is likely.
- Jie Wu
Title: Revisit to unstable homotopy theory
Abstract: In this 2-hour lecture, we will lead a tour for junior topologists to revisit unstable homotopy theory. The first half of lecture will start from a warm-up that gives an unpublished elementary combinatorial proof of generalized Hilton-Milnor theorem, and then propose a couple of open projects that junior researchers could investigate as further explorations. The second half of the lecture will start from a warm-up of explaining the distributivity law that gives connections for Hopf invariants, looped Whitehead products, looped degree maps and power maps, and then lead junior researchers to consider various problems on the structures of homotopy groups, from longstanding unresolved Moore conjecture and Barratt conjecture, to p-local hyperbolicity problem, periodicity problem and retraction problem, with moving further to propose many new questions on the extensions of strong-form of Kervaire invariant problem, structuring all homotopy groups into a single group, higher operations on homotopy groups via minimal models for infinite-groups and infinite-categories, and higher categorification of the Cohen groups.
- Jiawei Zhou
Title: Rational homotopy theory and Sullivan model
Abstract: In this talk, we begin by constructing a rational algebraic model for a topological space, then derive its minimal Sullivan model, which offers greater tractability and provides a more transparent and direct reflection of the homotopy data. Subsequently, we address the other direction: recovering the original space (up to rational homotopy equivalence) from its Sullivan model.
Taking spheres as our foundational example, we demonstrate how this correspondence faithfully encodes rational homotopy and homology for well-behaved spaces—such as simply connected spaces with finite-type cohomology. We will also explore the limitations of this approach when extended to more general cases. This leads to the open problem of when the realization preserves rational cohomology. If time permits, we will also discuss other algebraic methods for extracting topological information from Sullivan models.
Map